摘要

纖維增強混雜復合材料通過在單一基體中復合多種纖維類型，實現了強度、重量與成本的有效平衡。本研究聚焦彎扭復合載荷下碳/玻纖增強混雜復合材料的設計優化，采用有限元分析（FEA）與響應面法相結合的技術手段，對包括夾層結構和非夾層結構在內的12種不同鋪層構型進行分析，旨在確定最優鋪層角度和纖維體積分數，以最大化失效載荷，同時最小化材料成本與密度。

研究結果表明，[C3G]S、[C2G2]S、[CG3]S等夾層型鋪層構型展現出優異的強重比性能，其失效載荷均超過300牛；最優鋪層角度因鋪層構型而異，范圍介于12°至30°之間；提高碳纖維體積分數通常可提升失效載荷，但需與玻纖保持最佳配比平衡。本研究所得結論為工程師針對航空航天、汽車及結構工程等應用場景定制混雜復合材料提供了寶貴的設計指南。未來研究應重點開展實驗驗證工作，并將分析范圍拓展至沖擊、疲勞等更多載荷工況，以進一步提升混雜復合材料結構的可靠性。

1.簡介

纖維增強混雜復合材料是一類精密材料，通過在單一基體中整合多種纖維類型，充分發揮每種纖維的優勢并彌補各自的缺陷。因此，這類材料憑借其優異的性能和可定制化的使用特性，在多個行業中得到廣泛應用。在航空航天領域，混雜復合材料因其高比強度和耐久性，被用于制造飛機零部件；汽車行業將其應用于車輛部件，以實現減重增效、提升燃油經濟性；建筑領域則將其融入建筑材料，增強結構性能并延長使用壽命；此外，混雜復合材料還被用于自行車、網球拍、頭盔等運動器材的制造。

復合材料結構（如飛機機翼）通常承受彎扭復合載荷。王等人建立了不同扭彎比下機翼盒段的屈曲與后屈曲數學模型；穆克吉等人研究了變剛度薄壁復合材料梁在彎扭耦合工況下的靜力特性與穩定性；任等人探討了加勁鋼管在壓-彎-扭復合載荷作用下的靜力行為；帕圖埃利等人提出了一種有限元方法，可預測彎扭耦合梁結構的靜動態特性。

碳/玻纖增強混雜復合材料的優勢之一是抗彎強度的提升，這一現象被稱為正混雜效應。董和戴維斯對碳/玻纖增強環氧混雜復合材料的抗彎性能進行研究后發現：對于單向復合材料，當玻纖/環氧層合板位于受壓面時會產生正混雜效應，而位于受拉面時則以負混雜效應為主；對于夾層型混雜復合材料，碳/環氧層合板應作為蒙皮，玻纖/環氧層合板作為芯層。在拉/壓載荷作用下，層間碳/玻纖增強混雜復合材料的拉伸失效應變呈現+7.4%的正混雜效應，而壓縮失效應變則出現-6.4%的負混雜效應；對于層內碳/玻纖增強混雜復合材料，拉伸強度和壓縮強度分別實現了+17.8%和+39.6%的最佳協同效應。

由于混雜復合材料在復合載荷下的力學行為較為復雜，通常需要借助有限元分析（FEA）等數值方法，并通過數值模擬實現優化設計。莫阿澤德等人定義了結構效率指標和性能指數，用于綜合篩選影響層合薄壁復合材料梁靜動態性能的設計參數，所建立的設計圖表和簡化方法可作為選擇滿足剛度和質量要求的層合復合材料梁的工具——層合復合材料梁的關鍵設計參數包括層數、層合板厚度、纖維取向角、構成材料及橫截面形狀。蒙特等人以給定載荷下的最大位移最小化為目標，將鋪層取向作為設計變量，對復合材料試樣進行了優化。類似地，因方特等人針對彎扭復合載荷下的碳/玻纖增強混雜復合材料開展了優化研究。

第二代非支配排序遺傳算法（NSGA-II）是一種進化算法，通過非支配排序對解決方案進行排序，并利用擁擠距離指標保持種群多樣性，適用于解決多目標優化問題，能高效引導種群向帕累托前沿的均勻分布近似解進化。然而，當NSGA-II與FEA耦合時，由于每次NSGA-II迭代都需要更新FEA模型，導致多目標優化過程耗時過長，難以實際應用。董針對單向和多向混雜復合材料制定了多項設計規則，與NSGA-II優化相比，這些規則在以成本和重量最小化為目標函數的優化中，表現出更優的效率和效果。

本研究以彎扭復合載荷下滿足指定失效載荷為前提，對碳/玻纖增強混雜復合材料進行優化，旨在最小化材料密度和成本。研究首先確定了多種鋪層構型，并為每種構型明確了最優纖維取向；通過系統改變碳/環氧層和玻纖/環氧層的纖維體積分數，利用FEA模型計算失效載荷；隨后建立響應面模型，量化纖維體積分數對失效載荷的影響；基于該模型篩選出滿足失效載荷要求的潛在鋪層方案；最后評估所選構型的成本和密度，并構建帕累托前沿。

2.研究方法

2.1.材料

本研究中的混雜復合材料采用層間結構設計，以環氧樹脂為基體，碳纖維和玻璃纖維為增強體，每層均由高強度碳纖維或E-玻璃纖維單獨增強。纖維與環氧樹脂的材料性能基于文獻數據，具體如表1所示；復合材料的等效性能通過哈辛復合圓柱模型（Hashin’sCompositeCylindricalModel,CCM）推導得出。

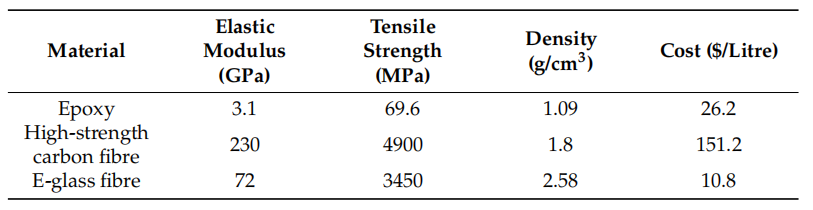
表1組分材料性能參數

纖維與環氧粘結劑之間的界面結合性能通過輸入材料性能參數間接表征，該參數源自文獻中的實驗數據。與玻璃纖維相比，碳纖維具有更高的界面剪切強度和潤濕性，這一特性已體現在所賦予的正交各向異性強度值中，與以往的建模方法保持一致。

本研究選用對稱角鋪設層序列，原因在于其比準各向同性層合板具有更高的強度和韌性，且不存在橫向層強度薄弱的問題。

2.2基于有限元分析（FEA）的模型

該模型為承受彎扭復合載荷的8層層合板結構。圖1展示了基于AutoCAD2023繪制的幾何形狀與載荷工況示意圖。由圖1可知，該復合材料板包含8個鋪層，每個鋪層厚度為0.25mm，層合板總厚度為2mm；復合材料試樣的長度和寬度分別為115mm和65mm。通過一個圓柱形加載壓頭對復合材料板施加預設向下位移，該加載壓頭位于笛卡爾坐標系（100,50）處（坐標原點如圖1所示）。

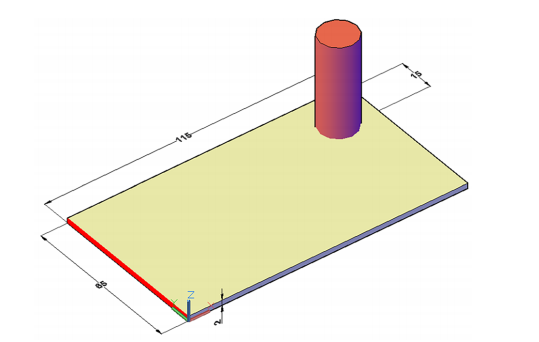
圖1

復合材料鋪層在AnsysACP模塊中定義。針對碳纖維/環氧層和玻璃纖維/環氧層兩類鋪層，分別設定正交各向異性材料性能及所有強度參數。基于上述失效模式假設，復合材料被建模為面體結構。參考圖1，約束x=0和y=0兩條邊緣，通過加載壓頭在z軸方向施加30mm的預設位移。仿真分析在AnsysMechanical中完成，采用與先前研究一致的技術路線。

碳/玻纖增強混雜復合材料的鋪層順序定義為從左至右對應第8層至第1層，其中C代表碳纖維/環氧層，G代表玻璃纖維/環氧層。例如，鋪層[C7G]表示第1層為玻璃纖維/環氧層，第2-8層為碳纖維/環氧層；該鋪層中玻璃纖維/環氧層位于試樣下表面，處于受壓狀態。

研究表明，受彎復合材料層合板的失效多始于受壓側。復合材料的壓縮行為較為復雜，可能存在多種失效模式：純壓縮失效、分層/剪切失效以及微屈曲或扭結失效。本研究采用羅-陳模型（Lo–Chimmodel）預測微屈曲或扭結引發的壓縮失效。

為確保有限元分析（FEA）結果的準確性與收斂性，對網格進行了加密處理。

2.3最優鋪層角度

本研究共考慮12種潛在鋪層方案，包括1種全碳纖維鋪層（[C8]）、1種全玻璃纖維鋪層（[G8]）以及10種混雜鋪層。其中混雜鋪層包含3種夾層結構鋪層（[C3G]S、[C2G2]S、[CG3]S）和7種非夾層結構鋪層（[C7G]、[C6G2]、[C5G3]、[C4G4]、[C3G5]、[C2G6]、[CG7]）。

針對每種鋪層方案，需確定使失效載荷最大化的鋪層角度（[(±θ)?]S）。以[C4G4]鋪層為例，在碳纖維體積分數（Vfc）為0.3、玻璃纖維體積分數（Vfg）為0.5的條件下，研究了不同鋪層角度對結構變形的影響，結果如圖2所示。數據表明，當鋪層角度為0°時，試樣產生顯著扭轉變形。

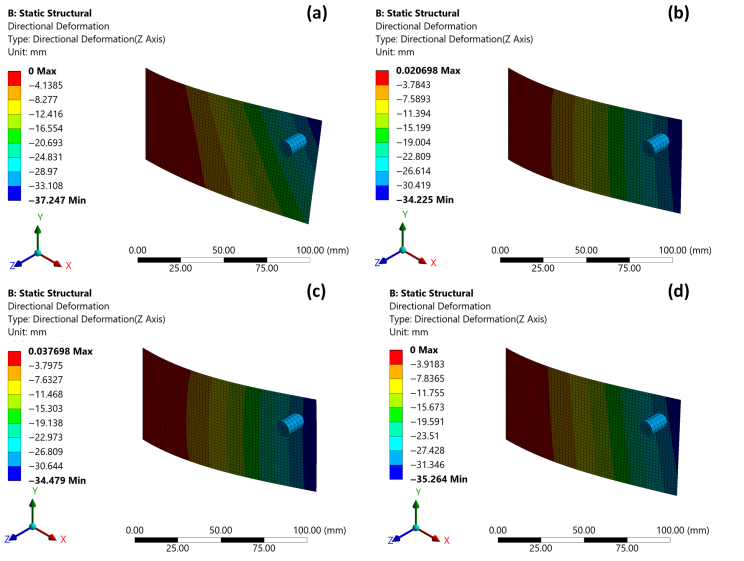
圖2

為進行對比分析，本研究對兩種準各向同性鋪層序列（[0/90/±45]S和[0/±45/90]S）與上述12種鋪層方案一并開展仿真分析。

圖3和圖4分別展示了第1層和第8層的最大失效判據分布。結果表明：當鋪層角度為0°或26°時，第1層的最大失效判據值高于第8層，說明失效將始于處于受壓狀態的第1層；當鋪層角度為45°或90°時，第8層的最大失效判據值高于第1層，表明失效將發生在受拉狀態的第8層。

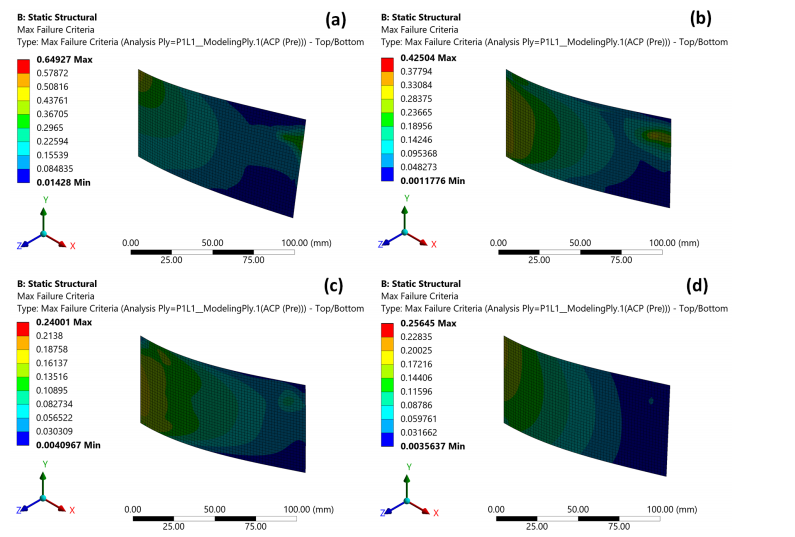
圖3

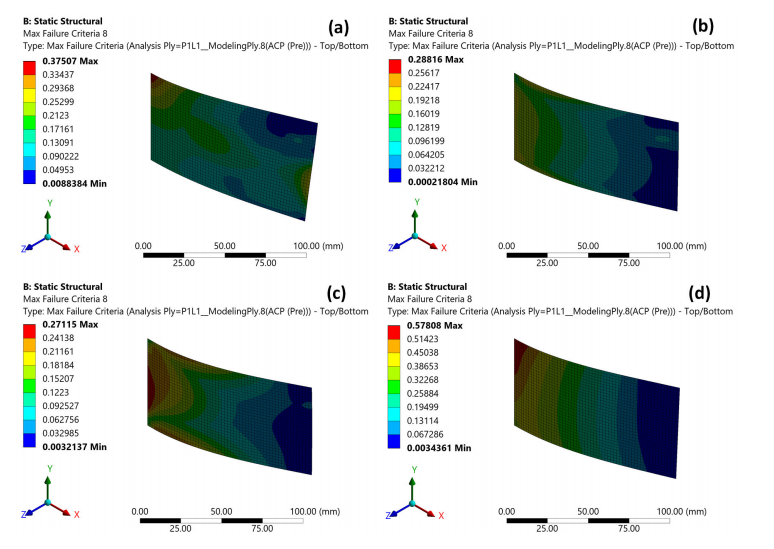
圖4

2.4響應面

圖5呈現了[C4G4]鋪層的破壞載荷與鋪層角度的關系曲線，據此可確定最優鋪層角度為26°。將鋪層角度設定為26°后，分別對碳纖維體積分數（Vfc）與玻璃纖維體積分數（Vfg）這兩個參數進行調控——二者均在0.3-0.65的范圍內分5個水平取值，并記錄各參數組合對應的破壞載荷。所得破壞載荷數據如表2所示，且可繪制成等值線圖（見圖6）。

由圖6可知，破壞載荷同時受碳纖維體積分數與玻璃纖維體積分數的共同影響。當碳纖維體積分數為0.3、玻璃纖維體積分數為0.3時，破壞載荷達到最小值；當碳纖維體積分數為0.65、玻璃纖維體積分數為0.5625時，破壞載荷達到最大值。此外數據還顯示，當玻璃纖維體積分數超過0.5625時，破壞載荷會隨玻璃纖維體積分數的增大而下降。

圖5

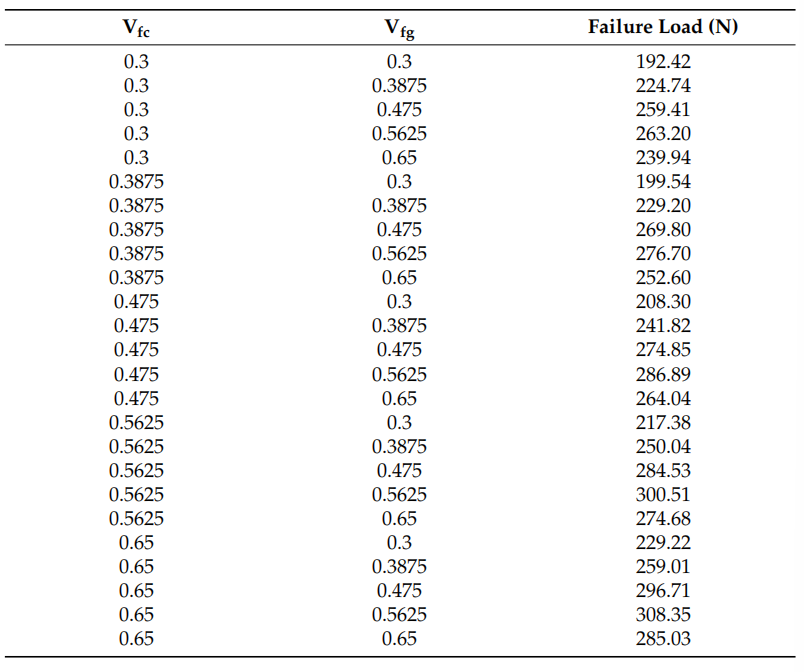
表2

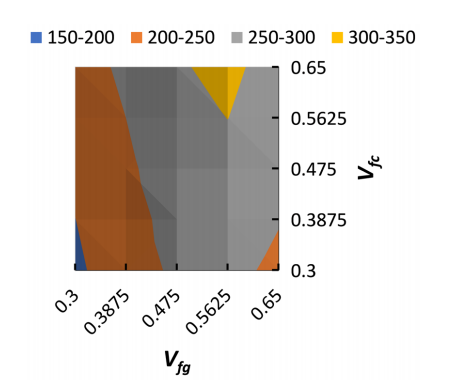
圖6

2.5備選方案確定

針對給定的目標破壞載荷，本研究通過調整碳纖維/環氧樹脂層與玻璃纖維/環氧樹脂層的纖維體積分數，得出每種特定鋪層方案對應的適配參數組合。由于該問題存在多組可行解，研究先將碳纖維體積分數（Vfc）設定為若干預設值（如0.3），再依據等值線圖調整玻璃纖維體積分數（Vfg），直至剛好滿足目標破壞載荷要求。一旦確定纖維體積分數參數，便基于對應鋪層方案明確材料構成，隨后借助表1中的材料性能數據計算出該方案對應的材料密度與成本。

3.結論

本研究采用有限元分析（FEA）與響應面法相結合的技術手段，完成了彎扭復合載荷下碳/玻纖增強混雜復合材料的設計優化，主要結論如下：

1.最優鋪層取向：性能最優的層合板鋪層角度介于12°至30°之間，具體數值隨鋪層構型的不同而有所差異。

2.優勢鋪層類型：與全碳纖維或全玻璃纖維層合板相比，[C3G]S、[C2G2]S、[CG3]S等夾層型鋪層構型展現出最高的強重比和成本效益。

3.纖維體積分數影響規律：破壞載荷對碳纖維體積分數（Vfc）和玻璃纖維體積分數（Vfg）均高度敏感；最優參數區間為Vfc=0.3–0.65且Vfg<0.5625，此范圍內可避免材料強度下降。

4.強度性能表現：性能最優的混雜鋪層方案在實現超過300N破壞載荷的同時，保持了相對較低的材料密度與成本。

5.失效機理特征：材料失效傾向于因微屈曲/扭結作用始于受壓側，而夾層結構構型可通過載荷重分布效應緩解此類失效風險。

6.設計應用價值：研究所提出的預測公式與等值線圖，為初步設計階段的鋪層取向選擇及纖維配比優化提供了實用技術指南。

7.未來研究方向：建議后續開展實驗驗證工作、納入層間脫粘效應分析，并將研究范圍拓展至沖擊、疲勞等其他載荷模式，以進一步提升混雜復合材料設計方案的可靠性。